Скин-эффект в аудио кабеле
(Что такое скин-эффект, и как правильно его бояться)
Баю-баюшки-баю,
Не ложися на краю —
Придет серенький волчок
И укусит за бочок!
Аудиофильская страшилка про скин-эффект
1. Страшное введение в ужасный скин-эффект
Как только заходит разговор на темы проводов и кабелей, так аудиофилы начинают пугать народ: в кабелях сидит страшный скин-эффект (у нас его называют поверхностный эффект), который вам весь звук испортит, если конечно не закажете у Великого Аудиофильского Шамана специальное заклинание для Великого Аудиофильского Духа. На вопрос: «А чем так страшен скин-эффект?» они бодро отвечают, что скин-эффект, он же поверхностный эффект, это распространение тока не по всему сечению провода, а только в его тонком поверхностном слое (скин-слое). При этом сопротивление провода увеличивается (т.к. используется только часть сечения провода), что и мешает жить. В доказательство вам приведут всех поголовно радиочастотников (у которых скин-эффект по применимости стоИт на втором месте после закона Ома и которые для борьбы с ним используют специальный провод — литцендрат: в нем множество тонких изолированных друг от друга проволочек скручены в жгут, и в нем ток не «отжимается» к поверхности провода – изоляция не дает), и даже на статью в Википедии. Но вот на вопрос: «Так это на высоких частотах, а как обстоят дела на звуковых частотах?», вразумительного ответа обычно не дают (аудиофилы вообще не любят заморачиваться с физикой и математикой, а просто используют ученые слова для придания солидности своим выдумкам). В лучшем случае скажут, что на частоте 20 кГц толщина скин-слоя равна 0,47 мм, типа вот сами и смотрите.
Я всегда считал, что влияние поверхностного эффекта на звуковых частотах для акустических кабелей сильно преувеличено (хотя в молодости я сам свивал по 8 проводов в литцендрат для использования в ультразвуковых генераторах мощностью 1…5 кВт на частоте примерно 22 кГц и мотал им дроссели — иначе грелись, заразы ). Что касается межблочников – там про скин-эффект вообще можно и не вспоминать. Однако личные убеждения к делу не подошьешь, поэтому давайте просто возьмем, и разберемся.
Прежде всего, ответьте на один простой вопрос (чур, в ответы в конце статьи не заглядывать!). В Википедии написано, что на частоте 10 кГц толщина скин-слоя в меди – того самого «тонкого поверхностного слоя, в котором протекает весь ток» — равна 0,66 мм (и это верно). Повторяю – толщина слоя считается от поверхности до центра проводника. Так вот, вопрос. Если диаметр проводника равен 1,0 мм, следовательно, радиус проводника равен 0,5 мм, а толщина скин-слоя – 0,66 мм. Еще раз: ток течет по толщине 0,66 мм, а проводник имеет толщину всего 0,5 мм – где берется еще 0,16 мм? Ведь там проводника уже нет, ток по воздуху течет, что ли?
На самом деле, вопрос некорректен, т.к. такой упрощенный подход к скин-эффекту, в этом случае неприменим. Тем не менее, именно таким подходом оперируют аудиофилы, когда пугают людей. Я объясню подробнее, но предупреждаю, что все равно придется упрощать. Неупрощенно это все видно из уравнений электромагнитного поля Максвелла, и в той же Википедии кратенько прописано. Если вы достаточно хорошо разбираетесь в высшей математике и теории поля, то вам и так все ясно. Если нет – то придется упрощать. Но так, чтобы не потерять правильность явления.
2. Страшный смысл ужасного скин-эффекта
Итак, упрощенно, но достаточно правильно.
Переменный ток, протекая по проводнику, создает внутри него переменное магнитное поле, которое воздействует на этот самый ток, уменьшая его тем сильнее, чем глубже в проводнике он течет. При этом по самой-самой поверхности протекает точно такой же ток, какой был бы без поверхностного эффекта (на постоянном токе), а чем глубже, тем ток меньше. Самое главное, что в каждом более глубоком слое сила тока во сколько-то раз меньше, чем в предыдущем (для ряда случаев это точно, для некоторых это очень-очень приближенно и зависимость является не геометрической прогрессией, а гораздо более сложной).
Если бы в проводнике было 5 слоев, то при уменьшении тока в каждом следующем слое в 1,5 раза, распределение тока по сечению проводника было бы такое, как показано на рисунке 1. Для простоты я все время буду считать, что ток на поверхности провода равен 1 ампер.
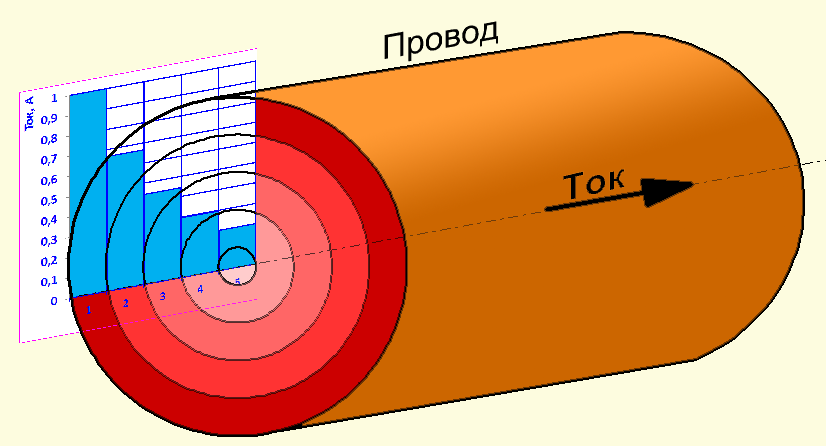
Если бы по проводнику протекал постоянный ток, то в каждом слое ток был бы равен 1 амперу и суммарный ток всего проводника был бы равен 5 ампер. На переменном токе из-за все большего уменьшения тока в глубинных слоях суммарный ток получается 1+0,6667+0,4444+0,2964+0,1975=2,6 ампера. Теперь допустим, что напряжение на концах проводника в обоих случаях (постоянный и переменный ток) одинаково и составляет 5 вольт (чтобы на постоянном токе через провод с R=1 ом протекал ток 5 ампер, а на переменном токе мы подаем точно такое же напряжение и смотрим что получится). Тогда по закону Ома:
- сопротивление для постоянного тока Rпост = 5В / 5А = 1 Ом
- сопротивление для переменного тока Rперемен = 5В / 2,6А = 1,92 Ом
То есть, из-за влияния скин-эффекта сопротивление проводника возросло примерно в два раза.
Это объяснение «на пальцах», но правильно передающее суть ситуации.
В дальнейшем я не буду рисовать сам провод и его слои, а буду показывать только график зависимости послойной плотности тока (величины тока в каждом слое) от глубины. На рис. 1 показано распределение тока только в левой половине провода – так было нагляднее нарисовать, да и в другой половине оно такое же. Вот как бы выглядел этот график для двадцатислойного распределения тока:

На самом деле слои имеют бесконечно малую толщину (и их самих бесконечно много), поэтому говорят не о величине тока в каком-то слое, а о плотности тока на какой-то глубине от поверхности (плотность тока j – это сила тока, деленная на сечение проводника, через которое он протекает, она измеряется в А/мм2). Поскольку бесконечно тонкие слои невозможно разделить между собой, то график превращается в линию (рис. 3).

Правда в таком виде график не такой наглядный и не все гуру с интернет-форумов его поймут. Поэтому я пока что порисую графики по слоям.
Теперь попытаемся ответить на вопрос, откуда взялось то определение про «тонкий поверхностный слой» в котором течет ток.
Допустим, наш проводник имеет очень большой диаметр (толщину). Сантиметров десять. И разбит на 100 слоев. Пропустим по нему переменный ток. Частоту тока будем увеличивать. На низкой частоте поверхностный эффект выражен не сильно, а по мере роста частоты ток все больше «уходит» из центра проводника (рис. 4). Напоминаю, что абсолютно все цифры на этих графиках – условны, это лишь иллюстрации. Пока что.



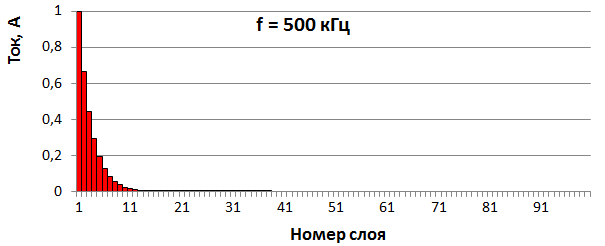
По последним двум графикам – 100 кГц и особенно 500 кГц действительно можно сказать, что ток течет только в тонком поверхностном слое. Вот смотрите: на частоте 500 кГц уже где-то в 12-м слое ток равен нулю. Так что про «тонкий поверхностный слой» все верно. Только вот есть несколько нюансов, про которые некоторые (даже гуру) либо забывают, либо вовсе не знают.
1. С ростом глубины плотность тока уменьшается по экспоненте (не всегда, но про эти случаи расскажу позже). Т.е. ток, он есть, просто очень маленький. Вот и кажется, что ноль на графике. Если последний график рисунка 4 построить в логарифмических координатах, то увидим, что ток на самом деле течет по всему проводнику (рис. 5). Нет такого места, чтобы тока не было. Только величина этого тока ну очень мала: пико-, фемто- и аттоамперы.

2. Экспоненциальная зависимость плотности тока от глубины (т.е. уменьшение тока в каждом следующем слое в одно и то же число раз) существует, только если толщина провода бесконечна. Исходная теория и выводится из предположения бесконечной толщины провода. Если толщина конечна, то в формулы вносятся поправки. В принципе, если толщина провода намного (в десятки раз) превышают толщину скин-слоя, то погрешность от применения формул, выведенных для бесконечно толстого провода мала, и этими формулами вполне можно пользоваться на практике. Но повторяю, толщина скин-слоя должна быть меньше толщины провода раз в 10. Для рис. 4 это последний вариант с частотой 500 кГц. На частоте 100 кГц погрешность уже есть, но ею еще можно пренебречь, а для частоты 5 кГц график уже совсем неправильный. Ну и ладно – это ведь иллюстрация, правильный график будет дальше.
Если толщина провода близка к толщине скин-слоя (или меньше него), то там используются уже совсем другие формулы (именно поэтому мой вопрос на засыпку про провод диаметром 1 мм не корректен). А «обычные» формулы неприменимы. Не потому, что ученые, которые их выводили – дураки. А потому, что их выводили как раз для такого случая. Именно этими формулами широко пользуются все высокочастотники – для них условие выполняется на все сто. А вот те, кто пытается использовать формулы, выведенные для одних условий (высокие частоты) там, где они не работают (низкие частоты) – вот те, наверное, дураки, или они просто вас обманывают. Про ситуацию, когда толщина провода соизмерима с толщиной скин-слоя – см. ниже.
3. Из рис. 5 видно, что примерно к трети толщины проводника сила тока уменьшается в миллион раз (напоминаю, это число – от фонаря!). Так что можно смело сказать, что ток там не течет. Но возникает пара вопросов – можно ли пренебрегать этим хоть и мизерным, но током, и где провести границу – типа тут ток еще течет, а глубже – уже нет. На оба этих вопроса есть один общий ответ. И его дает математика. Сила тока в проводе целиком – это сумма токов, текущих через каждый слой. Например, сумма высот всех столбцов на рис. 4 или 5. Сложили эти 100 чисел – получили общий ток провода. Поскольку количество слоев на самом деле бесконечно, то вместо суммы токов в слоях надо использовать интеграл (как предел суммы бесконечно малых) от плотности тока. Геометрически – это площадь под кривой на рис. 3. Такой вот криволинейной трапеции. Математически распределение плотности тока в проводнике можно записать:
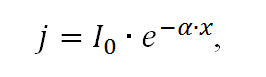
где Io — ток на самой-самой поверхности провода, α – некоторый коэффициент (на самом деле это коэффициент затухания электромагнитной волны; например, на рис. 3 α = 0,03); х – расстояние от поверхности в глубину провода.
Суммарный ток в проводе, он же площадь криволинейной трапеции, он же интеграл получается такой (учитывая, что толщина провода бесконечна):

Потерпите, еще совсем чуть-чуть математики, и заканчиваем с ней.
Если этот интеграл вычислить в общем виде, то получится, что он равен:

Величину Δ называют толщиной скин-слоя.
То есть весь этот ток в бесконечных слоях и бесконечно малой величины можно легко посчитать. Прикладной смысл полученной формулы показан на рис. 6: ток во всем проводе со скин-эффектом точно такой, как если бы скин-эффекта не было, а одинаковый ток величиной Io протекал бы не по всему проводу, а только по слою провода толщиной Δ, а в остальном проводе тока не было бы вообще. Геометрический смысл – площадь под синей линией равна площади под красной линией. Так что как на самом деле распределен ток в проводе в этом случае неважно, вполне можно считать, что абсолютно весь ток протекает через этот «тонкий поверхностный слой», толщиной Δ. На рис. 6 он составляет 33% от толщины провода – это не верно: толщина провода должна быть бесконечной. Но поскольку график бесконечной ширины нарисовать не так-то просто, я надеюсь, что вы меня за это простите. В реальности это действительно тонкий поверхностный слой на толстом-толстом проводнике.

Кстати, и условие, что толщина провода должна быть во много раз больше толщины скин-слоя, на рис. 6 не выполняется. Так что это не научный график, а просто иллюстрация – не пытайтесь с его помощью что-нибудь доказывать.
И еще. Обратите внимание, что на глубине, равной толщине скин-слоя Δ, плотность тока всегда уменьшается до значения примерно 36% от того, что на поверхности провода. Так что на самом деле через скин-слой протекает 63% всего тока, а остальной ток течет по всей оставшейся толщине провода, вплоть до самого его центра (для круглого провода цифры немного другие, но принцип тот же).
Повторяю, все это верно только если радиус провода больше толщины скин-слоя по меньшей мере в 10 раз.
Резюмируем.
1. На самом деле ток всегда течет по всему сечению провода.
2. Но сила тока через весь провод (сумма его по всем слоям провода) такая же, как если бы ток не изменялся по толщине провода, а оставался точно такой же величины, как и на поверхности (как постоянный ток), но протекал при этом не по всему сечению, а только по его «внешнему кольцу», толщина которого называется толщиной скин-слоя.
3. В идеале это абсолютно верно для провода бесконечно большой толщины (диаметра). В реальности все это верно с малюсенькой погрешностью, если радиус провода в десять и более раз превышает толщину скин-слоя. Если толщина скин-слоя и радиус провода соизмеримы, то все очень сильно меняется. Остается только факт, что плотность тока на поверхности провода выше, чем в центре. А насколько, и как это все распределено – это надо считать отдельно с учетом конечного радиуса провода. Вот этим и займемся.
3. Очень страшное кино страшный скин-эффект 3
А теперь пришла пора поговорить о несовпадении реальных условий возникновения скин-эффекта в аудиопроводах с идеальными. Так как же быть, если радиус провода 0,5 мм, а толщина скин-слоя – 0,66 мм?
Да очень просто. На самом деле, в «тонких» проводах (у которых радиус провода не в 10-20 раз больше толщины скин-слоя, как положено по высокочастотной теории, а примерно равен, а то и меньше него) другое перераспределение тока по толщине провода. Чем провод тоньше – тем поверхностный эффект выражен меньше. То есть, тем ток внутри провода распределен более равномерно. Пример показан на рис. 7.

Тут уже никак нельзя сказать, что ток течет «только через тонкий поверхностный слой». И понятие толщины скин-слоя здесь не применимо вообще!!!
А как же тогда я говорю о том, чему равна толщина скин-слоя, если в ситуации как на рис. 7 эта толщина больше радиуса провода? Дело в том, что для толщины скин-слоя существует формула:

Я не буду ее расшифровывать, потому что эта формула выведена как раз для условия бесконечно большой толщины провода. И она работает только если толщина скин-слоя, вычисленного по этой формуле, раз в 10 (а лучше в 20-30) меньше диаметра провода. Если провод «тонкий», то формула не работает! И тот, кто ею в такой ситуации пользуется – ошибается! Под словами «не работает» я имею ввиду, что говорить, будто весь ток течет по сечению провода, вычисленному по этой формуле – неправильно (см. вопрос на засыпку в начале статьи – именно в этом и заключается подвох). Это глубина на которой электромагнитная волна в этом материале затухнет в е=2,7182… раза, если не будет волны, отраженной от задней стенки (т.е. в очень-очень толстой железке). Это формула для материала, а не для объекта!!!
Когда говорят «толщина скин-слоя», то практически всегда (если не прибавляют слово «реальная» или «действительная») речь идет о числе, полученном по этой формуле. Вот так и получается толщина скин-слоя 0,66 мм при радиусе провода 0,5 мм. Да в меди всегда на частоте 10 кГц толщина скин-слоя 0,66 мм! Она получается из этой формулы! Чтобы эта формула была применима, надо чтобы диаметр провода был как минимум 13 мм (радиус болше 6,6 мм), что дает нехилую площадь сечения 136 мм2 – и при этом формула толщины скин-слоя только-только начинает работать!
Итак, если толщина провода соизмерима с толщиной скин-слоя (вычисленного по той формуле), то одновременно происходит два важных явления:
1. Чем тоньше провод, тем меньше разница между плотностью тока на поверхности и в центре (поверхностный эффект выражен слабее).
2. Распределение плотности тока по толщине провода описывается не экспонентой, а другим выражением.
На рис. 8 приведены графики РЕАЛЬНОГО распределения тока по круглому медному проводу на частоте 20 кГц, когда толщина скин-слоя, вычисленная по формуле, составляет 0,47 мм и примерно совпадает с радиусом провода.

Пять линий на графике соответствуют «наиболее ходовым» сечениям провода. Как видно, у провода с сечением 0,75 мм2 поверхностный эффект практически отсутствует. Это как раз тот случай, когда радиус провода 0,49 мм совпадает с толщиной скин-эффекта (как раз выходит, что весь ток течет через этот слой – а других слоев-то и нет!). С ростом сечения, а значит и толщины провода, скин-эффект проявляется все ярче.
Тонкой коричневой линией показана экспонента – та зависимость, которая справедлива для провода, толщина которого намного больше толщины скин-слоя (я их рисовал все время для простоты иллюстраций). В самом начале (на поверхности проводника) график реального распределения плотности тока совпадает с экспонентой. А потом расходится все больше – это сказывается конечная и небольшая толщина провода, та самая поправка к формулам, о которой я говорил. Видите – в центре провода разница между линиями большая, и «высокочастотной» формулой пользоваться нельзя. Кстати, в реале ток через провод (площадь под графиком) получается больше, чем по «классической высокочастотной» формуле. Это значит, что влияние скин-эффекта как минимум преувеличено.
Спустя некоторое время мне пришло в голову перестроить этот график по-другому: показать, какая часть от всего тока в проводе протекает через «тонкий поверхностный слой» провода круглого сечения. И я сделал это, рис. 8_1. В нижней части рисунка показан тот же график, но «растянутый» в его начальной области, чтобы лучше можно было оценить ситуацию на самой поверхности провода. Как и предыдущий, график построен для частоты 20 кГц на которой скин-эффект выражен наиболее сильно. Кстати, хорошо видно, что линии на графике не прямые. Их искривление вызвано не только поверхностным эффектом, но и тем, что по мере углубления в провод, площадь сечения каждого из его «колец» уменьшается, при этом уменьшается и ток, протекающий по всему такому «кольцу».

Как пользоваться графиком? Очень просто. Например, для провода сечением 8мм2 (черная линия) через 50% толщины протекает 90% тока. Учитывая, что радиус провода 1,6мм, то выходит, что по части провода толщиной 0,8мм от поверхности к центру течет 90% всего тока (весь ток протекает по «кольцу» 0,8мм, а вовсе не 0,47мм, как следовало бы из толщины скин-слоя в меди!). Можно грубо считать, что практически весь ток протекает по «внешнему кольцу» в половину толщины провода, а его середина практически не работает. У провода сечением 4мм2 практически весь ток (90% всего тока) протекает по толщине в 60%, т.е. примерно 0,7мм от поверхности. У проводника сечением 0,75мм2 90% тока протекает по «внешнему кольцу» толщиной 70% от радиуса провода, примерно равному 0,34мм.
Выходит, раз для провода сечением 8мм2 «работает» 50% диаметра, то его сопротивление возрастет в два раза? Так в лоб считать нельзя. У нас же провод круглого сечения, это цилиндр. Посмотрите на рис.1. Допустим, что у нас «работают» участки 1-3 (это 60% толщины, которые соответствуют проводу с сечением 4мм2). Оцените визуально площадь сечения «внешнего кольца» и оставшейся центральной области. Оставшаяся «не работающая» область имеет маленькую площадь сечения, поэтому общее эффективное сечение провода уменьшается не так уж сильно. Еще раз: тот факт, что «работает» всего 50% радиуса провода означает 75% от его сечения. Да и то, там протекает не весь ток, а просто его значительная часть. И сам ток распределен по сечению неравномерно. Поэтому оценка изменения сопротивления провода будет очень-преочень грубой. Хотя, для провода сечением 8мм2 сопротивление как раз и увеличивается в два раза, но это просто совпадение чисел.
Этим графиком неудобно пользоваться для определения сопротивления и затухания в проводе (для этих величин информация будет чуть позже). Зато можно оценить влияние состояния поверхности провода на протекание по нему тока. Вот пример. Допустим, мы сравниваем два кабеля сечением 4мм2. Один из них чисто медный, второй – посеребренный. Также допустим, что толщина серебряного слоя составляет 35мкм (это как толщина фольги на печатной плате, такой слой серебра на самом деле толстый и кабель очень дорогой). Считаем. Радиус провода 1,13мм и толщина покрытия составляет 3% от радиуса. Для провода сечением 4мм2 по толщине 3% от поверхности протекает 9% от всего тока. Удельное сопротивление серебра примерно на 15% меньше, чем у меди. Следовательно, разница в этих кабелях такова: у посеребренного провода для 9% от всего тока мы уменьшили сопротивление на 15%. Сопротивление всего посеребренного провода на частоте 20 кГц благодаря серебру уменьшилось примерно на 1,2% по сравнению с чисто медным. И стОит ли платить за это в 15 раз дороже? (На самом деле у серебра толщина скин-слоя на 7% меньше, чем у меди, поэтому через серебряное покрытие пройдет немного большая часть тока, не 9%, а где-то 9,5% и общее сопротивление уменьшится тоже немного сильнее, не на 1,2%, а на 1,25%) Или другой пример. Допустим, неполированный медный провод сечением 4мм2 имеет шероховатость Rz=10мкм (к сожалению, я не нашел значений шероховатости для аудиокабелей, но судя по общему машиностроению, это значение завышено). Это составляет 0,9% от радиуса и по этому кольцу протекает 3% от всего тока. Полировка провода уменьшит сопротивление этого участка и улучшит прохождение тока (может быть даже раза в полтора). Правда, на остальные 97% тока полировка провода никак не повлияет.
4. Страшное влияние ужасного скин-эффекта на звук
Ну вот, наконец, и те результаты, ради которых все затевалось.
В интернете существует много разных сообщений, типа «я посчитал и получил число». Поэтому чтобы вы не сомневались в правильности моих вычислений, я описал их немного подробнее здесь: Расчет скин-эффекта в круглом проводе.
Поскольку вычисления сложные, я их делал в программе Mathcad (как и для рис. 8). Но переносить результаты в Excel и строить по ним графики мне было лень (это довольно громоздко), и я взял графики прямо из Маткада. Поэтому они получились не такими красивыми, как предыдущие т.к. предназначены для ученых а не для презентаций.
Далее представлены графики зависимостей от частоты некоторых параметров, связанных с сопротивлением кабеля из круглого медного провода длинной 2х10 метров (в смысле от усилителя до колонки 10 метров, а суммарная длина провода туда-сюда составляет 20 метров) определенного сечения. Сечения использовались такие: 0,75 мм2; 1,5 мм2; 2,5 мм2; 4 мм2; 8 мм2. Они вписаны как числа в выражениях слева от графиков. Сечение 8 мм2 на самом деле стандартным не является, я его выбрал для сокращения числа графиков: оно лежит между двумя стандартными значениями – 6 мм2 и 10 мм2. Так что для одного из этих кабелей все будет чуть больше, а для другого – чуть меньше.
Первый график – самый страшный (надо же пугать народ ужасным скин-эффектом!).
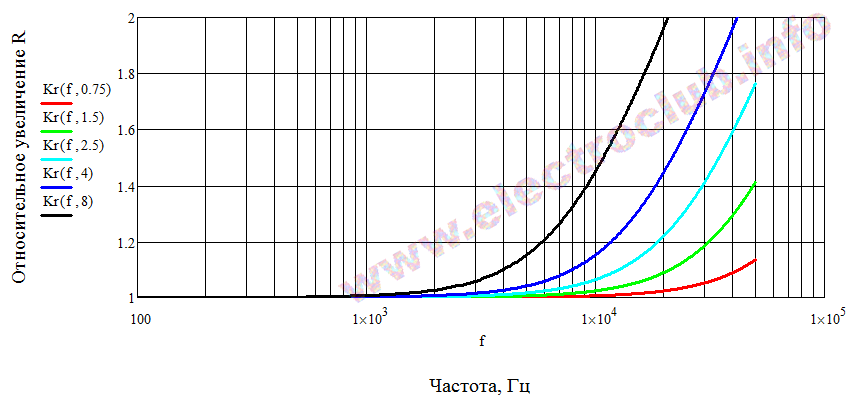
Относительное увеличение сопротивления – это по сравнению с постоянным током. Грубо говоря, получается оно так. Например, провод сечением 1,5 мм2 на постоянном токе имел сопротивление 1 Ом, а на частоте 50 кГц его сопротивление стало равным 1,4 ома — вот вам и зеленая кривая на графике. А провод сечением 8 мм2 на постоянном токе имел сопротивление 0,1 Ом, а на частоте 20 кГц его сопротивление выросло вдвое и стало равным 0,2 ома – вот и получилось на этой частоте число 2 у черной кривой.
Как видим, влияние скин-эффекта тем сильнее, чем больше диаметр (сечение) провода. На тонкие провода он влияет совсем мало (и этим пользуются, изготовляя литцендрат из множества тонких проводочков).
Но график на рис. 9 – это «специальный пугательный график». Им могут воспользоваться аудиофилы, чтобы пугать народ: вот, сморите, ваш самый толстый провод увеличивает сопротивление вдвое! Чтобы этого не случилось, надо покупать специально заколдованный против скин-эффекта провод по $1000 метр. На самом деле все не так страшно. Подумаешь, ну возросло сопротивление в 2 раза – у толстого провода оно изначально было мизерным. А ноль — его сколько не умножай, все равно нулем останется. И в доказательство этого, вот следующий график.

Итак, рис. 10. Видите? Толстый провод, который так сильно подвержен поверхностному эффекту, имеет сопротивление в миллиомы. 40 миллиом на постоянном токе и 80 миллиом на частоте 20 кГц. Ровно в 50 раз меньше сопротивления нагрузки. Так что можно не бояться. Провода меньшего диаметра имеют большее сопротивление и оказывают большее влияние на передачу тока. Но они меньше подвержены скин-эффекту, и, несмотря на то, что влияние самого провода больше, влияние скин-эффекта становится меньше. Это хорошо видно на следующем графике.

Здесь показано опять же относительное затухание, вносимое кабелем (напоминаю, длинна кабеля 10 метров от усилителя до колонки) при подключении активной нагрузки 4 Ома. Относительное – т.е. по сравнению с постоянным током, чтобы видеть влияние скин-эффекта в чистом виде. Итак, в самом плохом случае, АЧХ на 20 кГц упадет на 0,1 дБ. Поскольку это намного меньше чувствительности слуха на такой частоте, то вопрос о слышимости скин-эффекта можно закрыть. Кстати, на нагрузке с бОльшим сопротивлением, влияние поверхностного эффекта будет меньше.
Специально для любителей автозвука с элементами маньячества. Для популярной автомобильной нагрузки 2 ома и сечения кабеля 15мм2 (10 метров длины от усилителя до колонки) затухание на частоте 20 кГц увеличится по сравнению с низкими частотами не более чем на 0,25 дБ. Так что тоже совсем не страшно.
Ну а теперь – абсолютные значения затухания, вносимые кабелем с учетом поверхностного эффекта. Нагрузка 4 ома, длина кабеля 10 метров.
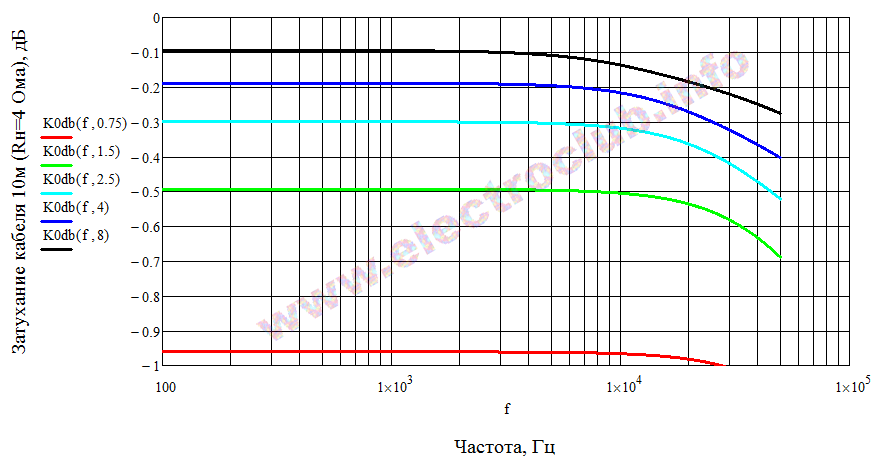
Для провода сечением 8 мм2 скин-эффект начинает быть «слышным-по-графикам» («слышу то, что вижу») примерно с 5 кГц. Реальным ухом он не слышен вообще. А вот величиной затухания в 0,5 дБ при применении кабеля сечением 1,5 мм2 уже наверное пренебрегать не стОит. На таком расстоянии наверное, лучше использовать кабель потолще. Хотя разница между 2,5 мм2 и 4 мм2 на слух практически незаметна.
Ну и последняя аудиофильская страшилка – влияние скин-эффекта на межблочник. Там тоже применяются всяческие дорогие аудиофильские решения, чтобы скин-эффект не пришел и не испортил весь звук. Посмотрим, с чем они там борются (ВНИМАНИЕ! Сечения другие, «более межблочные»!).

Заклиная многими долларами Великого Аудиофильского Духа, в межблочнике успешно побеждают поверхностный эффект, составлявший стотысячные доли децибела! Ура, товарищи!
Если входное сопротивление блока больше, то скин-эффект проявляется меньше. Выходное сопротивление блока-источника сигнала больше 10 Ом уменьшает влияние скин-эффекта раз в 10 и более. Причем все это совершенно бесплатно.
5. Страшное состояние поверхности провода и его влияние на ужасный скин-эффект
Тот факт, что плотность тока на поверхности проводника выше, чем в середине (называемый поверхностным эффектом), вызвал к жизни еще две аудиофильские страшилки, связанные с состоянием поверхности провода:
- шероховатость поверхности провода (надо ли полировать провод?);
- наклеп (сжатие) на поверхности провода.
Хотя, может быть, эти страшилки возникли самостоятельно. На самом деле и здесь все сильно-пресильно преувеличено, а в некоторых вещах даже сами аудиофилы не определятся – хорошо это или плохо. Здесь я не буду обсуждать эти явления, чтобы не загромождать статью. А статью про эти дела напишу отдельно чуть позже и поставлю здесь на нее ссылку. Пока что только скажу вот что: на звуковых частотах высота шероховатости провода (промышленного, аудиофилы при необходимости могут сделать специальный очень плохой провод в котором все будет влиять) настолько мала по сравнению с толщиной скин-эффекта, что об этом можно и не думать. С наклепом — там немного сложнее, но тоже абсолютно ничего страшного.
6. Совсем нестрашные заключения, выводы, уточнения
0. Главное! Поверхностный эффект вызывает только лишь масенькое увеличение сопротивления на высоких частотах и больше ничего! Т.е. при одном и том же напряжении на выходе усилителя на частоте 20 кГц звук будет на 1,1% тише, чем на низких частотах. 1,1% — это как раз те 0,1 дБ, что на рис.11, а для кабеля сечением 2,5 мм2 затухание на частоте 20 кГц равно 0,7 дБ – это 0,8% снижения громкости. Вот и все. Всего лишь небольшое изменение тембра. Да и то на частоте, которую даже не все слышат! На частоте 10 кГц, на которой чувствительность слуха уже заметно снижается, из-за скин-эффекта АЧХ падает на 0,15%. Всего лишь.
То, что говорят о «перепутывании» звука при распространении по кабелю многочастотного сигнала – это перепутывание происходит в мозгах того, кто говорит (или он специально вас запутывает, чтобы что-то вам продать). Кабель – высоколинейная штука, и «каждая из частот» в нем распространяются независимо. Каждая со своей толщиной скин-слоя. Каждая со своим эффективным сопротивлением кабеля. Только и всего. Импульсные сигналы тоже не «перепутываются». Импульсные сигналы можно рассматривать во временнОй области, тогда читаем главу «Переходные процессы с цепях с поверхностным эффектом». Там много сложной математики, но все сводится опять же к росту сопротивления. Также их можно рассматривать в частотной области – как набор сигналов с разными частотами. Такой подход возвращает нас к уже рассмотренным графикам. Так что ничего кроме небольшого роста сопротивления кабеля на высоких при скин-эффекте не происходит! Повторяю, чечь идет о звуковых частотах. Что происходит на телевизионных частотах нас волновать не должно!
1. А почему же тогда в технике столько говорят про скин-эффект? Потому, что мы живем в высокочастотный век. Возьмем не такую уж и высокую частоту 100 МГц (сравните ее с тактовой частотой процессора своего компьютера или смартфона). Это FM диапазон и самое начало телевизионного. А в компьютерной технике эту частоту уже давно и не вспоминают. Так вот, толщина скин-слоя в меди на этой частоте составляет 7 микрон! Это почти в 10 раз меньше толщины человеческого волоса! На такой частоте сопротивление жилы антенного кабеля (провода сечением 0,2 мм2) возрастает в 20 раз – а вспомните, что кабель прокладывается иногда на десятки метров! Даже по тонкой дорожке печатной платы ток течет не по всему сечению, а примерно по половине. Поэтому на ВЧ не рекомендуется облуживать дорожки: заметная часть тока будет протекать не в меди, а по слою припоя, у которого сопротивление в 4 раза выше (и по нижней стороне печатного проводника, который медный, что радует). А вот серебрить – это неплохо. Вот на таких частотах и начинают сказываться всякие вещи, типа влияния шероховатости поверхности провода на его сопротивление. На более высоких частотах скин-эффект становится настолько сильным, что ток начинает распространяться не по проводам, а как вода: по трубам – волноводам, отражаясь от стенок и не попадая внутрь металла.
Вот вам и распространение тока по тонкому поверхностному слою. А ведь у нас сейчас чуть ли не каждое третье устройство – высокочастотное. Со скин-эффектом. И на гораздо более высоких частотах, чем 100 МГц, приведенные в примере.
Углубившись в высокие частоты, мы необоснованно забыли энергетиков. На частоте 50 Гц толщина скин-слоя равна примерно 1 см. Поэтому даже самый толстый провод в нашем радиолюбительском трансформаторе этот эффект не ощущает. А вот когда провод становится толщиной в руку… В электрических машинах большой мощности (десятки-сотни киловатт и больше) скин-эффект начинает портить жизнь – повышается активное сопротивление провода и снижается КПД машины. И борются с этим делом: используют шины (проводом это уже назвать сложно) не круглого сечения, а прямоугольного. При этом во-первых, увеличивается площадь поверхности по которой протекает ток (т.е. сопротивление снижается), во-вторых, в тонком проводе скин-эффект выражен меньше. В третьих, работать с такими шинами технологичней. На частоте 50 Гц речь идет не о «тонком поверхностном слое», а о повышении сопротивления провода, хотя это тоже неприятно и не полезно. Правда, есть от него и польза: повышение пускового момента асинхронного двигателя с глубоким пазом — целиком заслуга поверхностного эффекта.
Вот в этих случаях скин-эффект – дело серьезное. А на звуковых частотах на малых мощностях его бояться не надо.
2. Итак, скин-эффект совсем не так страшен, как его пытаются представить аудиофилы. Если не прокладывать кабели длинной во многие десятки метров, то он ниже порога слышимости в колоночном кабеле, и в 1000 раз меньше порога слышимости в межблочном.
Если все же нужна длина кабеля в 100 метров, то тут 2 варианта: либо просто чуть-чуть поднять тембр и скомпенсировать те 0,2 дБ завала АЧХ, либо (что предпочтительнее с инженерной точки зрения) передать сигнал по межблочнику, а усилитель поместить в этих самых 100 метрах от источника сигнала непосредственно возле нагрузки. И колоночный кабель будет иметь длину 1 метр. Кстати, на длине кабеля 100 метров (общая длинна провода выходит 200 метров), затухание на частоте 20 кГц по сравнению с низкими частотами, вызванное скин-эффектом составляет примерно 0,8 дБ для сечений провода 6…16 мм2, а для кабеля 50 мм2 завал на 20 кГц составляет 0,5 дБ. Так что и тут немного.
3. На самом деле величина влияния скин-эффекта меньше, чем искажения АЧХ кабеля, вызванные его индуктивностью и емкостью.
4. Приведенные расчеты произведены для круглого цельного, т.е. одножильного провода. Если же провод многожильный, то надо вносить поправку. Чисто качественно поправка оценивается так. Если жилы туго скручены и контакт между ними идеальный, то с многожильным проводом происходит все один-в-один как с одножильным. Если контакт между жилами очень плохой (либо они окислены, либо неплотно скручены и между ними есть просветы), то получаем литцендрат с практически отсутствующим поверхностным эффектом. В реале ситуация находится где-то посередине, следовательно, в реальном кабеле скин-эффект может быть чуть меньше рассчитанного выше. Изменение геометрии провода (плоские и проч. провода) несколько уменьшает скин-эффект, но если его и так не слышно, то стОит ли платить больше?..
5. Расчетные формулы выведены для одиночного провода. Обычно акустические кабели двойные, и там присутствует еще и эффект близости, перераспределяющий ток по сечению проводника. Оценка влияния эффекта близости показала, что его влияние ничтожно. Вот в трансформаторах с КПД выше 99% этот эффект заметно влияет и чтобы получить такой большой КПД, с ним приходится бороться. В нашем случае им вполне можно пренебречь, т.к. он дает отклонение от полученных цифр примерно на 3…20% (в зависимости от конструкции кабеля).
6. Для межблочника результаты получились даже слегка завышенными (если он «однопроводный», т.е. центральная жила – это прямой провод, а обратный провод – это экран). Ну, там и так практически полный ноль.
Так что – не бойтесь, никакой скин-эффект к вам не придет! А если и придет, то вы его даже и не заметите.
А как же аудиофилы про него все время говорят? А вы посмотрите, КАК они говорят про него:
Аудиофил: Вы же знаете, существует скин-эффект.
Инженер: А давайте посчитаем, насколько он влияет. Или измерим.
Аудиофил: Нет-нет!!! Считать-мерять ничего не надо: ни расчеты, ни измерения ничего не значат! Мы же знаем, что он есть, значит надо бороться, специальные дорогие провода делать…
PS. Этот текст получился каким-то очень злым. Но тому есть причина. Когда я готовил его, я прочитал в интернете несколько десятков статей по поводу кабелей. Чего там только не было! С умным видом нести столько чуши!.. Хотя, мне показалось, что большинство авторов сами не очень в этом разбираются, а повторяют чьи-то слова. А сколько всяких псевдонаучных теорий и наукообразных измышлений! Один только учет волнового сопротивления кабеля чего стОит! Не спорю, волновое сопротивление архиважно для телевизионщиков – антенный кабель с неправильным волновым сопротивлением будет плохо работать. Но то на частоте 100 МГц! А на звуковых частотах оно начнет влиять только для кабеля длинной начиная где-то с пары километров. В общем, складывается впечатление, что кабель – самая важная часть аудиокомплекса, и не важно, какие у вас усилитель, колонки и CD-плеер, главное – какие у вас кабели, и вот их подобрать неимоверно трудно. А и правда – это усилитель один раз купил, и все, а кабелями можно торговать и торговать. И получать за них хорошую денюжку… Самая страшная ложь – это полуправда. В ней очень трудно отделить одно от другого. И вот такой полуправды я и начитался по самое немогу.
Узнать про реально измеренный скин-эффект и некоторые другие свойства кабелей можно здесь: Реальный скин-эффект в кабелях.
В статье Акустический кабель – измерения приведены хорошие измерения нескольких аудиокабелей. Скин-эффект, индуктивность, ёмкость.
07.07.2013 — 18.07.2013 — 14.08.2013