Расчет скин-эффекта в круглом проводе
Знаете, почему люди перестали писать на заборах? Потому, что появился интернет. И теперь в нем пишут все то же самое, что раньше на заборах писали.
Довольно часто люди, успешно освоившие таблицу умножения на 3 и на 9, начинают публиковать в интернете свои расчеты и статьи, на них основанные. Собственными глазами видел ветку на одном из солидных форумов, где автор описывал свою «теорию». Правда автор не дружит с физикой и не знает математики (поэтому дифференциальные уравнения, описывающие его объект, которым его «теория» в корне противоречила, он просто игнорировал). Тем не менее, ветка жила около года и набрала пару десятков страниц.
А раз такое дело, то и мне довольно часто приходится доказывать, что то, что я пишу, взято не с потолка, а так оно и есть. То есть приводить источники моей информации, формулы, расчеты и прочее. По моим наблюдениям больше всего требуют указывать источник информации те люди, которые сами не прочь приврать, или уверенно утверждать то, чего на самом деле они не знают наверняка. И от других они ожидают того же, вот и требуют обосновывать чуть ли не каждое слово.
Здесь я покажу, откуда взялись результаты расчетов, приведенные в статье Скин-эффект в аудиокабелях.
Если вы откроете Википедию на странице, посвященной скин-эффекту (напоминаю, что это название заимствовано из английского языка, у нас в ходу термин «поверхностный эффект«), то увидите там математические формулы со страшными зюкозябрами. Дело в том, что этот эффект описывается разделом высшей математики, называемым «Теория поля». Его как раз и придумали именно для расчета физических полей. Так что тут и физика, и математика в одном флаконе. Надо сказать, что этот раздел математики — один из трудных. Во-первых потому, что математика-то — высшая. Во-вторых — потому, что те операторы, из которых состоят эти формулы и уравнения (роторы, дивергенции, потоки вектора и проч.), сами составлены из довольно сложных математических выражений. Как возведение в целую степень — это несколько умножений, и для его изучения нужно умножением владеть, так и операции теории поля состоят из интегралов, дифференциальных уравнений в частных производных и т.п. Если хотите — посмотрите в той же Википедии что такое дивергенция и оцените ее «изящную простоту». Есть и третья трудность — эта математика используется намного реже, чем «обычные интегралы», поэтому менее привычна. И еще одна сложность — если физический смысл «обыкновенных интегралов» и «обычных, всем понятных дифференциальных уравнений» довольно ясен, то тут с ним гораздо сложнее, и по крайней мере для меня это неприятно.
Так что с детсадовской математикой расчеты не повторить. Даже конечные формулы содержат довольно сложные функции комплексного переменного, которые есть лишь в специальных математических программах (т.к. «обычные» люди с такими функциями в жизни не сталкиваются). Я использовал MathCad.
Для получения рабочих формул скин-эффекта в проводах и построения графиков я использовал учебник Теоретические основы электротехники Л.А. Бессонова, том 2 «Электромагнитное поле», изд. Гардарики, 2001 г. Если кто-то не знает, кто такой Л.А. Бессонов, значит он либо не учился в техническом ВУЗе, либо изучал там электротехнику «на детском уровне» — для неэлектротехнических специальностей. Учебник Бессонова — это №1, его даже не все преподаватели понимают, настолько он подробный и глубокий.
Чтобы ничего не переписывать вручную, вот вам сканы, откуда все взялось. Здесь выведены те формулы, которыми я пользовался.

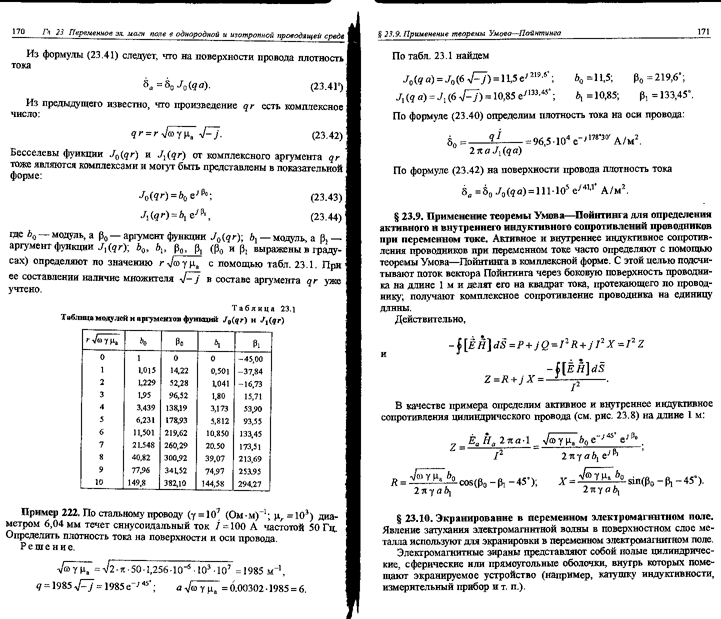
Если вы считаете, что формулы выведены неверно — разработайте свои и внесите исправления! 
07.07.2013